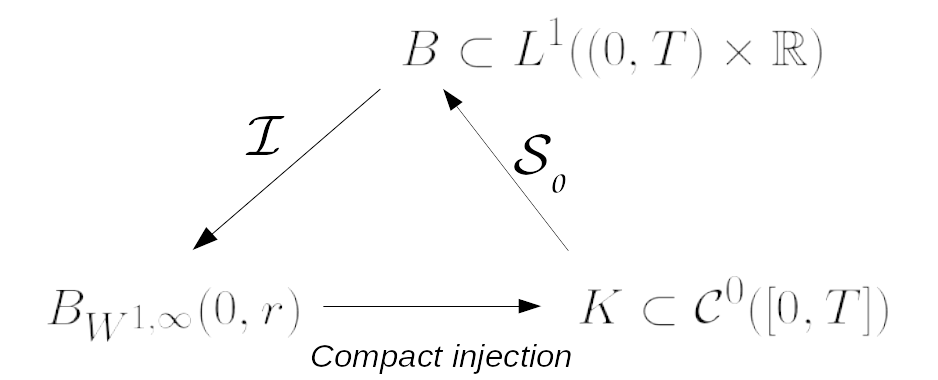
An abstract existence result for generalised Hughes’ model
Presented in Roma, Bangalore, Rouen and Tours
About me
I have a post-doctorate position in the Laboratoire Jacques Louis Lions in Paris. My research mostly focus on first order non-linear equations, you can find more about it in the research section. These equations can model the pedestrian flow in evacuation contexts. You can find results of simulations in the simulation section. Apart from the theoretical research, I also create synthesizers and scenography. These activities have their respective sections.
Research
Topics
- Discontinuous scalar conservation law - entropy solutions, dissipative germs, finite volume schemes.
- Macroscopic pedestrian flow models - non-linear coupling, fixed point arguments, splitting methods.
- Discontinuous Hamilton-Jacobi-Bellman equations - viscosity solutions, flux-limited solutions, finite difference schemes.
- Eikonal equation - Monge solutions, fast marching methods.
Presentations and publications
Pedestrian crowd models
Introductive presentation in Nouant-Le-Fuzelier
Existence and numerics for Hughes' model
Presented in Orleans and Valparaiso
A numerical scheme for the discontinuous Eikonal equation
Presented in Besançon
On the correspondence between Hamilton-Jacobi equations and scalar conservation laws.
Presented in Besançon
Macroscopic pedestrian flows: from Hughes’ model to mean field games.
Presented in Montpellier
Teachings
I teach mathematics and computer science in the university of Tours and the Supinfo school. Here is a list of the subject I taught:
- Linear algebra (Supinfo), Algebra III (Université de Tours)
- Analysis III (Université de Tours)
- Geometry (Université de Tours)
- Python programming (Université de Tours), C programming (Supinfo)
- Internet of things and embedded systems (Supinfo)
- Mathematical reasonning (Université de Tours), Mathematical tools for biology students (Université de Tours)
- Advanced SQL (Supinfo)
- Supply chain and software engineering (MECEN, Université de Tours)
Supports de cours
Applied graph theory
For MECEN students
Projects and ressources
Hughes2d software
Hughes2d is an open-source Python package for simulation pedestrian crowds in two dimensions. The package is designed to compute approximations of the Hughes model, a macroscopic model – there are no particles here, the crowd is represented by a density function– coupling two non-linear partial differential equations.
Lava flow on LED strip
The main idea of this project is to represent a flow of lava descending a constant slope on a programmable LED strip. This comes from an idea for the scenography of a music festival (Les ilots éléctroniques).
Musical instruments
The musical instruments I make are synthesizers inspired by wind instruments. The Polyclav is a numeric modular synth made to be compatible with the DM48 midi harmonica from Lekholm instruments. The Soubasynth is a synth inspired by the sousaphone. The Brassynth is an improved and portable version of the Soubasynth compatible with trombone and trumpet mouthpieces. The Soubasynth and the Brassynth both use a Bela board. This constructor made a post about my instruments on their blog.
Soubasynth
Brassynth
Polyclav
Scenography
Pole dance platforms with wheels
Scenography for a fanfare show
LED signs for a music festival
Metal jellyfish for a techno event
Giant teapot for a music festival
Scuttle lights for a music festival
Contact
You can contact me by e-mail at theo.girard /@/ math.cnrs.fr
Bureau : 5028
Bâtiment Sophie Germain, Campus Grands moulins
8 Place Aurélie Nemours
75013 Paris, France