Théorie des graphes
(En construction)
Introduction
La théorie des graphes est une branche des mathématiques qui étudie les relations entre les objets (appelés sommets ou nœuds) et les connexions entre eux (appelées arêtes ou arcs). Elle est utilisée dans de nombreux domaines comme les réseaux sociaux, les systèmes de transport, les circuits électriques et l'analyse de données.
Pour manipuler les graphes visuellement : https://d3gt.com/index.html
Définitions de base
Graphe
Un graphe G est un ensemble de sommets V et un ensemble d'arêtes E. Formuellement, un graphe est défini comme une paire G = (V, E), où :
- V est un ensemble de sommets (ou nœuds),
- E est un ensemble d'arêtes, chaque arête étant une paire non ordonnée de sommets dans V (pour un graphe non orienté) ou une paire ordonnée de sommets (pour un graphe orienté).
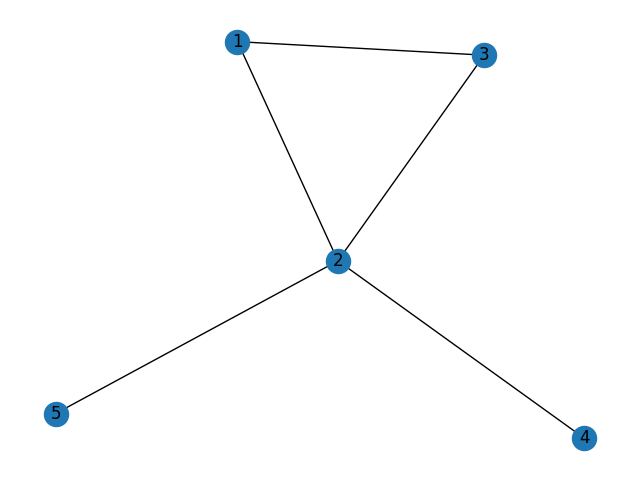
V = { 1,2,3,4,5 }
E = {(1,2), (1,3), (2,3), (5,2), (2,4)}
Graphe orienté et graphe non orienté
- Graphe orienté : Un graphe dans lequel les arêtes sont dirigées, c'est-à-dire que chaque arête est représentée par un couple ordonné de sommets (u, v), où u est le sommet de départ et v le sommet d'arrivée.
- Graphe non orienté : Un graphe dans lequel les arêtes ne sont pas dirigées, c'est-à-dire que chaque arête est simplement un ensemble de deux sommets {u, v}, sans ordre particulier.
Exemple de graphe orienté
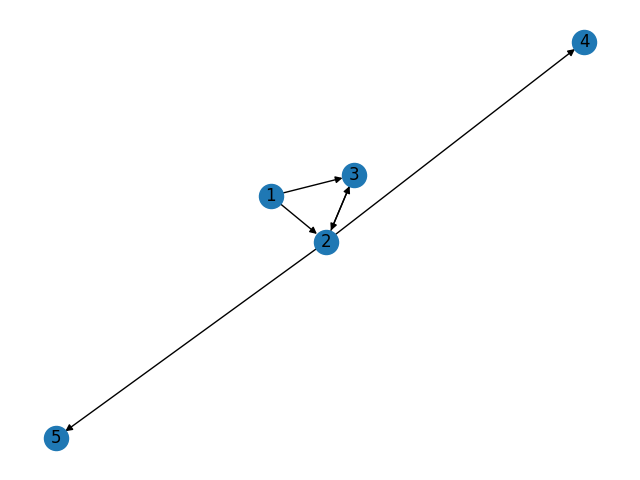
V = { 1,2,3,4,5 }
E = {(1,2), (1,3), (2,3), (3,2), (5,2), (2,4)}
Graphe pondéré
Un graphe pondéré est un graphe (orienté ou non) auquel on ajoute une fonction \(\omega : E \longrightarrow \mathbb{R}\). On appelle \(\omega\) la fonction de poids.Le poids d'une arrête peut être interprêté comme le temps nécessaire pour parcourir l'arrête ou, plus généralement, comme un coût à payer pour traverser l'arrête.
Exemple de graphe pondéré non orienté
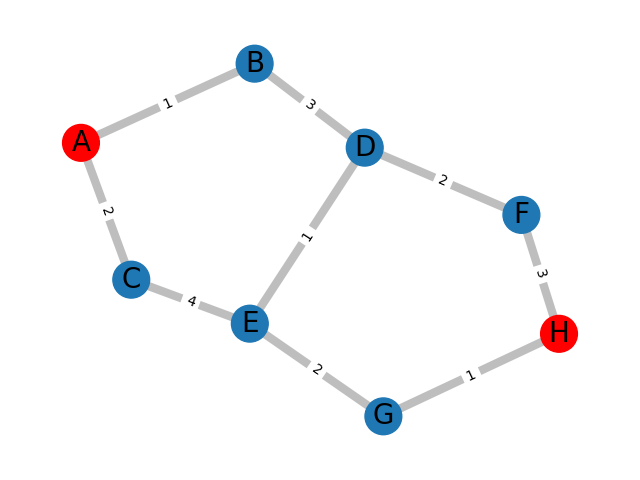
V = { A,B,C,D,E,F,G,H }
E = {(A,B), (A,C), (C,E), (B,D), (D,E), (D,F), (F,H), (H,G), (E,G)}
\( \omega((A,B)) = 1, \; \omega((B,D)) = 3, \; \omega((E,G)) = 2,\) ...
Voisins et degré d'un sommet
Soit \(A \in V\). Dans le cas d'un graphe non orienté, on définit :
- l'ensemble des voisins \(\mathcal{V}(A)\) est l'ensemble des sommets \(B \in V\) tels que \( (A,B) \in E \),
- le degré d'un sommet \(A\), noté \( \mathbf{deg}(A) \), est le nombre d'arêtes qui touchent \(A\). C'est à dire le cardinal de \(\mathcal{V}(A)\).
Dans le cas d'un graphe orienté, on parle plutôt de :
- l'ensemble des prédécesseurs d'un sommet \(A\) notés \(\mathcal{P}(A)\) défini par : \[ \mathcal{P}(A) := \{ B \in V \textrm{ tels que } (B,A) \in E \}, \]
- l'ensemble des successeurs de \(A\) noté \(\mathcal{S}(A)\) défini par : \[ \mathcal{S}(A) := \{ B \in V \textrm{ tels que } (A,B) \in E \}. \]
Chemin et cycles
Un chemin est une séquence de sommets dans laquelle chaque sommet est adjacent au suivant. Un cycle est un chemin dont le premier et le dernier sommet sont identiques.
Dessiner un graphe en python
Dans ce cours, les graphes seront représentés avec les bibliothèques python networkx et matplotlib.
#On importe les deux bibliothèques
import networkx as nx
import matplotlib.pyplot as plt
#On créé le graphe
G = nx.Graph() #Non-orienté
#G = nx.DiGraph() #Orienté
#On créé les noeuds
G.add_node(1)
G.add_nodes_from ([2,3,4,5])
#On ajoute les arrêtes entre les noeuds
G.add_edge(1,2)
e = (2,3)
G.add_edge(*e) # the * unpacks the tuple
G.add_edges_from([(1,2),(1,3),(2,4),(2,5)])
#On dessine le graphe
nx.draw(G, with_labels =True)
#On peut sauvegarder la figure
plt.savefig("basicgraph2.png")
#Ou juste l'afficher
plt.show()On obtient le résultat suivant :

Théorèmes
Quelques théorèmes de base de la théorie des graphes.
Parcours de graphe DFS/BFS
Dans de multiples problèmes nous sommes amenés à parcourir un graphe, c'est-à-dire aller de sommets en sommets en suivant les arrêtes du graphe. Par exemple, pour savoir si deux sommets sont connectés ou pour savoir si le graphe comporte un cycle. Pour parcourir un graphe, il existe principalement deux manières de procéder : l'exploration en profondeur DFS (Depth First Search) ou l'exploration en largeur (Breadth First Search). Ces deux algorithmes ont des temps de calcul très variables (et complémentaires) en fonction de la forme du graphe.
Parcours en profondeur DFS
Le parcours en profondeur consiste à parcourir le graphe en utilisant la stratégie suivante : si je suis à une intersection, je choisis une arrête arbitrairement; je continue ce chemin jusqu'à être coincé ou jusqu'à ce que j'aie trouvé ce que je cherche. Si je suis coincé, je reviens sur mes pas jusqu'à la dernière intersection. Cette stratégie correspond à la stratégie bien connue pour trouver la sortie d'un labyrinthe : toujours prendre à gauche. Voici deux illustrations de la stratégie DFS pour trouver un chemin du sommet A au sommet F à gauche et pour trouver un chemin du sommet A au sommet H à droite.
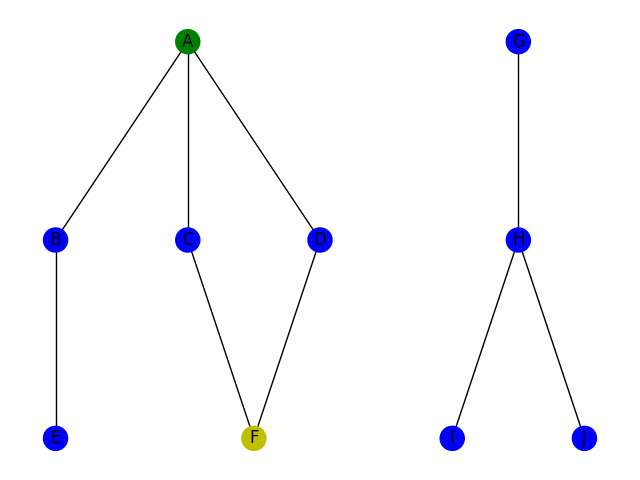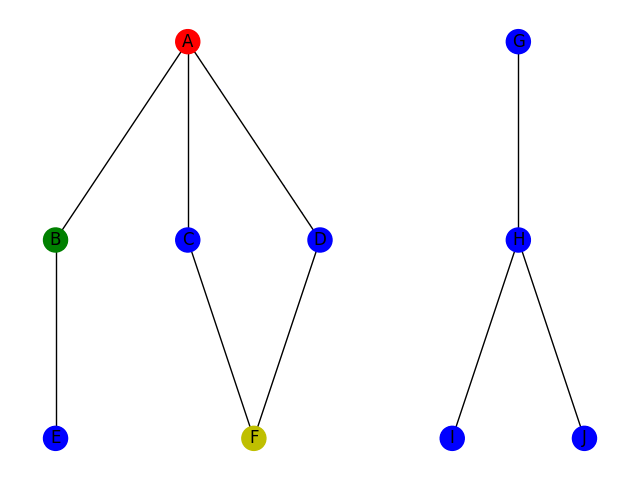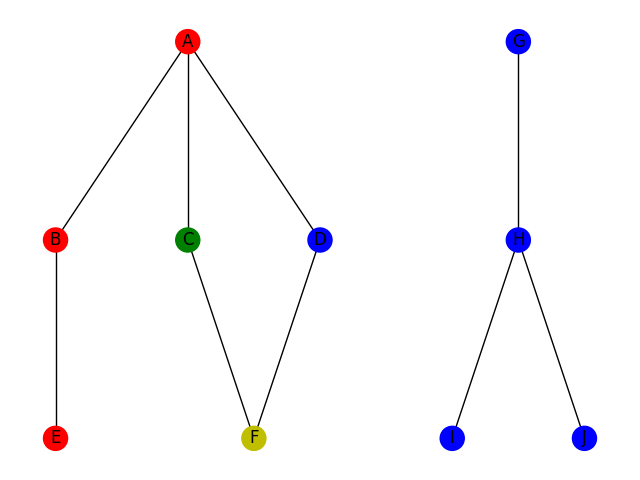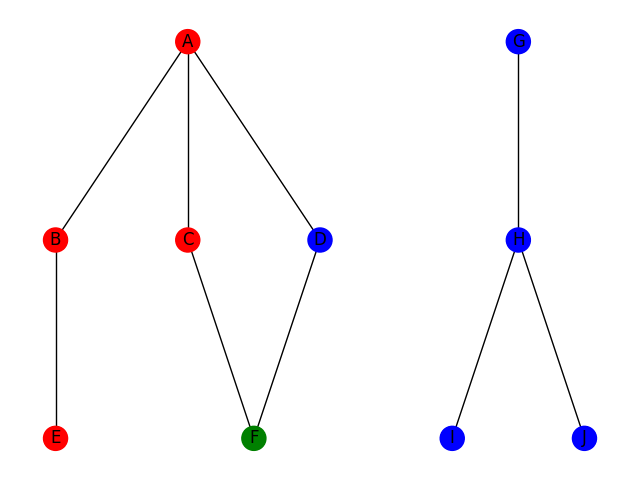
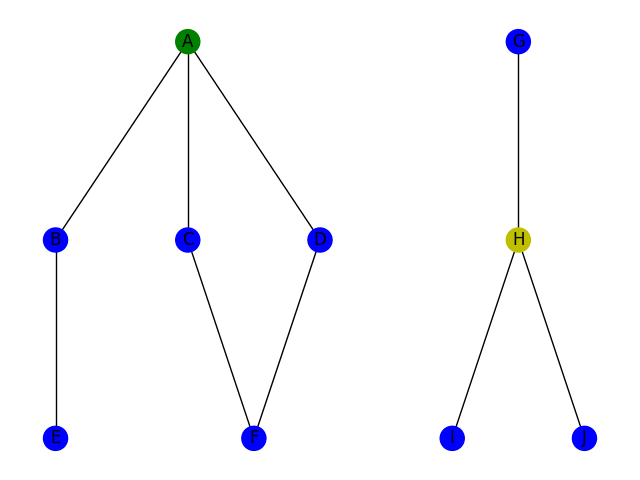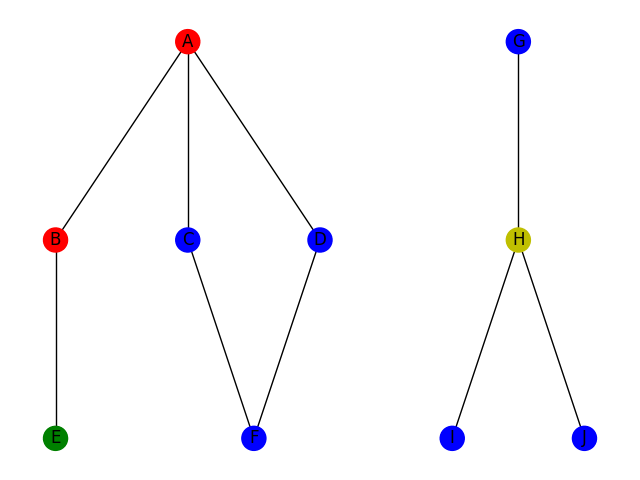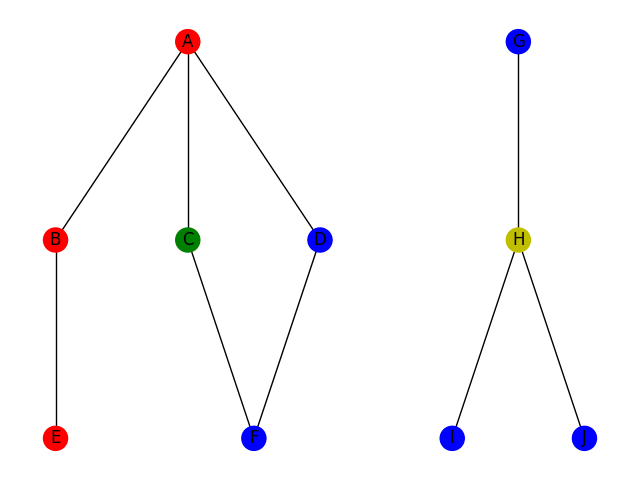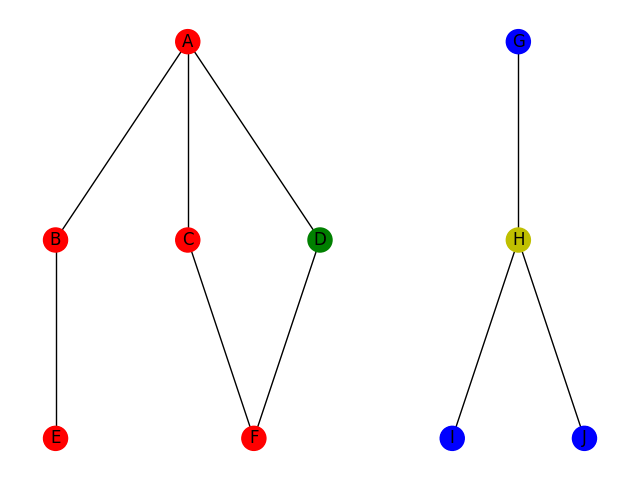
D'un point de vue code, on utilise la plupart du temps un algorithme récursif (bien qu'un algo itératif soit envisageable). Voici une implémentation possible en python, en supposant l'existence d'un objet Graphe avec une méthode Voisins qui renvoie la liste des voisins d'un sommet.
def explorer(Graphe, sommetActuel, pointArrivee, parcourus):
parcourus.append(sommetActuel) #On garde en mémoire les sommets par lesquels on est passé.
if(sommetActuel == pointArrivee): #Condition d'arrêt : on a trouvé le sommet qu'on recherche.
return True
for voisin in Graphe.Voisins(sommetActuel): #On parcourt les voisins du sommet.
if(voisin not in parcourus): #On vérifie qu'on n est pas déjà passé par là.
if(explorer(Graphe, voisin, pointArrivee, parcourus)): #On continue l'exploration de ce chemin tant qu on n'est pas bloqué.
return True
return False #Si on n a trouvé aucun voisin qui n'a jamais été parcouru, on abandonne ce chemin.
Parcours en largeur BFS
Le parcours en largeur consiste à utiliser la stratégie suivante : on explore tous les voisins du point de départ, on liste tous les voisins de ces voisins qui n'ont pas encore été parcourus; on réitère le procédé sur cette nouvelle liste de voisins jusqu'à trouver ce qu'on cherche ou jusqu'à ce qu'on ne trouve plus de voisin non parcourus. Cet algorithme correspond à un parcours par "génération" de voisin. En effet, si on définit la distance de voisinage entre deux sommets A et B comme le nombre d'arrêtes minimal pour passer de A à B, alors le parcours BFS va parcourir tous les sommets à distance 1 du point de départ puis tous les voisins à distance 2 et ainsi de suite. Voici une illustration dans le même contexte que le parcours DFS pour comparer.
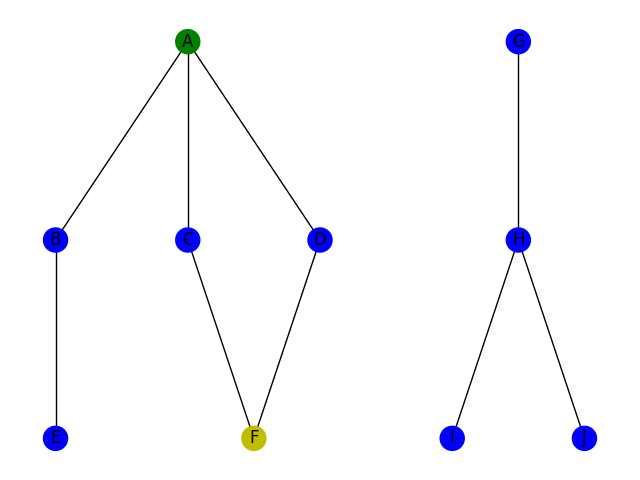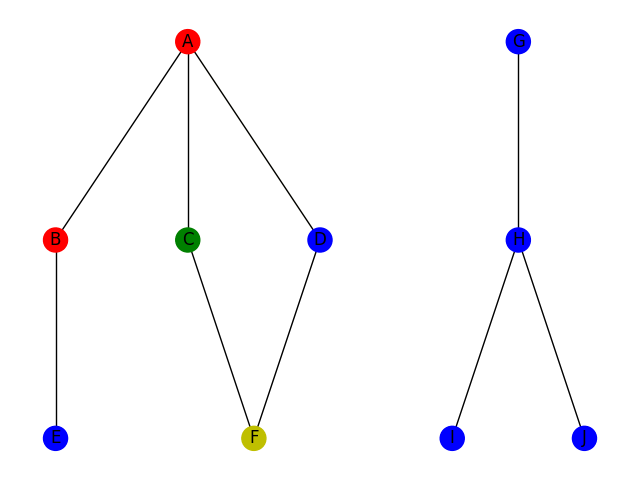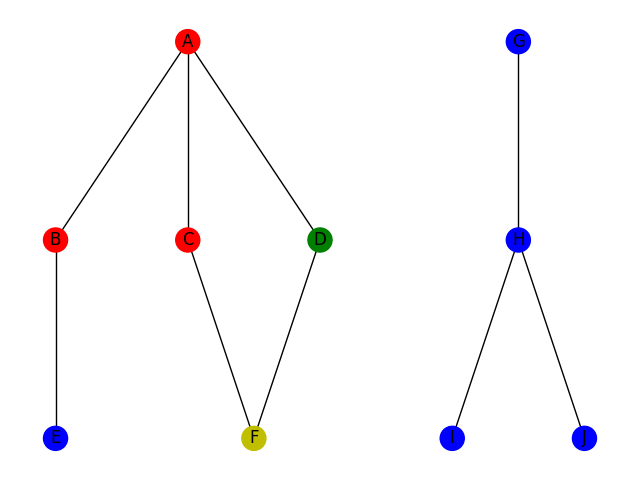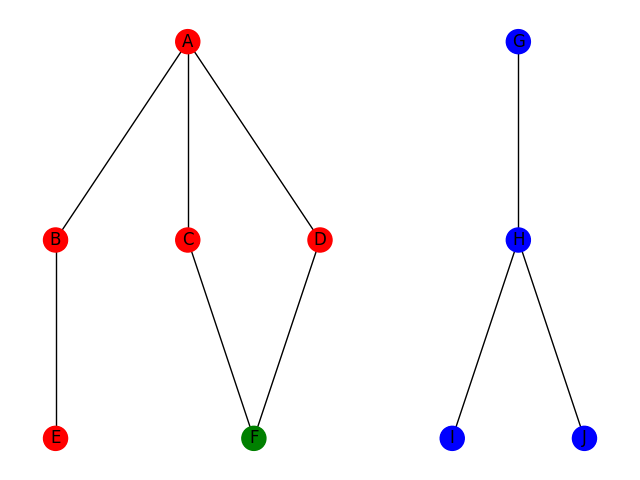
Le parcours BFS est généralement implémenté comme un algorithme itératif à la différence du DFS. En voici une implémentation possible en python, en supposant l'existence d'un objet Graphe avec une méthode Voisins qui renvoie la liste des voisins d'un sommet.
def explore(Graphe, pointDepart, pointArrivee):
parcourus = []
nodesToexplore = [pointDepart] #La liste des noeuds à explorer qui sera tenue à jour à chaque itération.
while(len(nodesToexplore) > 0):
newNodes = []
for node in nodesToexplore:
if(node == pointArrivee): #Condition d'arrêt : si on a trouvé le point d'arrivée, on arrête.
return True
parcourus.append(node)
for P in Graphe.Voisins(node):
if(P not in parcourus):
newNodes.append(P) #On remplit la liste newNodes de tous les voisins non parcourus de la prochaine génération.
nodesToexplore = newNodes
return False #Si on a plus aucun noeud à explorer, c'est qu'il n'existe pas de chemin reliant le point de départ au point d'arrivée.
Programmation dynamique et Bellman-Ford
Le principe de la programmation dynamique est un principe algorithmique pour optimiser la quantité de calculs à effectuer lors de la résolution de problèmes d'optimisation. L'idée générale est de diviser le problème d'optimisation en une multitude de sous-problèmes plus faciles à résoudre et de stocker les résulats de ces sous-problèmes plutôt que de résoudre ces problèmes à chaque itératon. L'exemple le plus fréquent d'application du principe de la programmation dynamique est l'algorithme de Bellman-Ford.
Algorithme de Bellman-Ford
On se donne le graphe pondéré suivant :

L'algorithme de Bellman-Ford permet de trouver efficacement un tel chemin. Il fonctionne de la manière suivante : en partant de A, on évalue le coût nécessaire pour aller à chaque voisin de A. Ici, pour B, on trouve 1 et pour C, 2. On réitère le processus pour les voisins de B puis les voisins de C en selectionnant la valeur de coût minimale trouvée. On continue cet algorithme jusqu'à ce qu'on couvre tout le graphe.
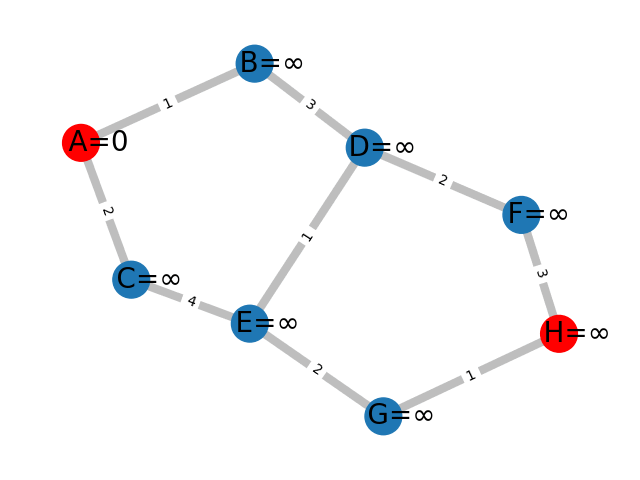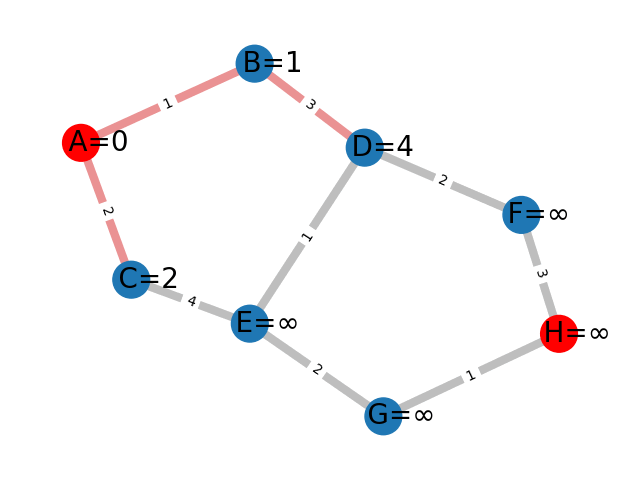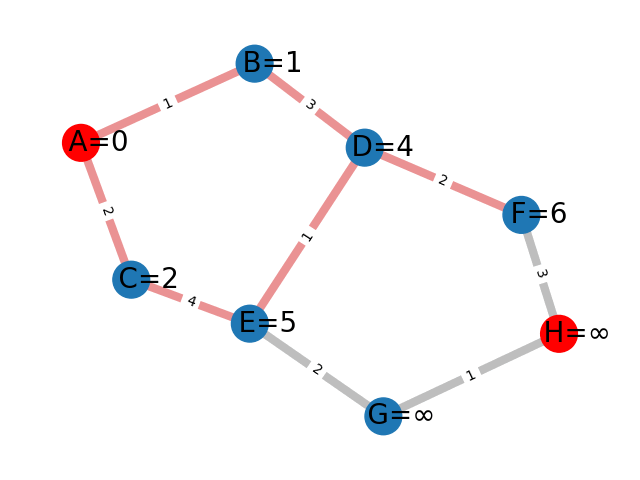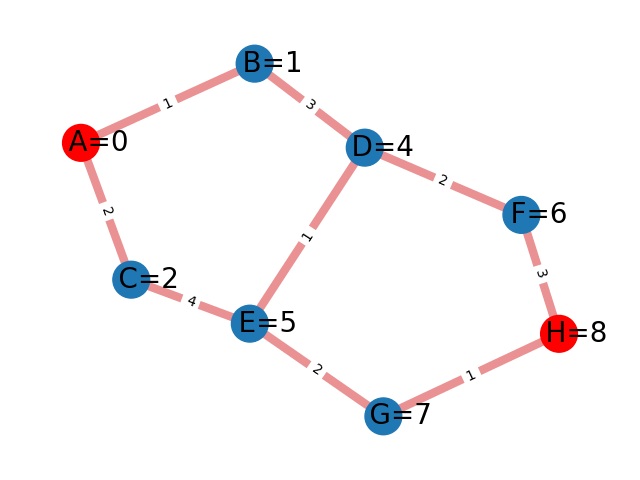
En python, on pourrait implémenter l'algorithme de Bellman-Ford ainsi:
Parcourus = []
ValeurDict = {}
def evaluerCout(Graphe, pointactuel):
Parcourus.append(pointactuel)
valeurMinimale = float("inf")
for voisin in Graphe.voisins(pointactuel):
if voisin in Parcourus:
if ValeurDict[voisin] + Graphe.poidsArrete(pointactuel, voisin) <= valeurMinimale:
valeurMinimale = ValeurDict[voisin] + Graphe.poidsArrete(pointactuel, voisin)
ValeurDict[pointactuel] = valeurMinimale
for voisin in Graphe.voisins(pointactuel):
if voisin not in Parcourus:
evaluerCout(Graphe, voisin)
Parcourus.append(pointDepart)
ValeurDict[pointDepart] = 0
for voisin in Graphe.voisins(pointDepart):
evaluerCout(Graphe, voisin)
Flot maximal et coupe minimale
Problème de flot maximal
Avant d'énoncer le problème du flot maximal, on introduit deux définition supplémentaires.Réseau de flot
Un réseau de flot est un graphe pondéré orienté \( G = (V,E,c) \) qui vérifie :
- les poids des arrêtes sont strictement positifs (i.e. \( c > 0 \) ),
- si \((A,B) \in E \) alors \((B,A) \notin E \).
Flot associé à un graphe \(G\)
Soit \( G = (V,E,c) \) un réseau de flot. Soient \( s, t \in V \) deux sommets particuliers que l'on nomme respectivement la source et le puits. On suppose que \(s\) n'a pas de prédécesseur et que \(t\) n'a pas de successeur dans \(G\). On dit que la fonction \( f : E \longrightarrow \mathbb{R} \) est un flot de \(s\) à \(t\) si :
- pour toute arrête \((A,B) \in E,\; 0 \leq f((A,B)) \leq c((A,B))\),
- pour tout sommet \(A \in V,\) si \(A \neq s \) et si \(A \neq t\), alors \[ \sum\limits_{B \in \mathcal{P}(A)} f((B,A)) = \sum\limits_{B \in \mathcal{S}(A)} f((A,B))\] où \( \mathcal{P}(A), \mathcal{S}(A) \) sont respectivement l'ensemble des prédécesseurs de \(A\) et l'ensemble des successeurs de \(A\).
La valeur \(|f|\) d'un flot \(f\) est définie par : \[|f| = \sum\limits_{B \in \mathcal{V}(s)} f((s,B)) = \sum\limits_{A \in \mathcal{V}(t)} f((A,t)).\]
Si on se donne un réseau de flot \(V,E,\omega\), un sommet source \(s\) et un sommet puits \(t\), le problème du flot maximal est donc de trouver un flot \(f\) de \(s\) à \(t\) de valeur \(|f|\) maximale.
Algorithme de Ford-Fulkerson
L'algorithme de Ford-Fulkerson permet de trouver un flot maximal lorsque l'algorithme termine (attention il existe des cas où l'algorithme ne termine jamais). Le principe de l'algorithme repose sur l'utilisation d'un graphe résiduel d'un flot \(G_f \). Si on cherche le flot maximal sur \(G = (V,E,c)\), le graphe résiduel \(G_f\) d'un flot \(f\) est un graphe pondéré orienté \(G_f = (V, E_{r_f}, r_f )\) (\(G_f\) a donc les mêmes sommets que \(G\)) où \(r_f\) est défini par : \[ \forall (A,B) \in V^2, \;\; r_f((A,B)) := \left\{ \begin{matrix} c((A,B)) - f((A,B)) & \textrm{ si } (A,B) \in E \\ f((B,A)) & \textrm{ si } (B,A) \in E\\ 0 & \textrm{sinon} \end{matrix} \right. \] et \(E_{r_f} = \{ (A,B) \in V^2, \textrm{ tels que } r_f(A,B) > 0 \} \).
On utilise alors l'algorithme suivant :
- on initialise le flot \(f\) comme nul;
- tant qu'il existe un chemin \(\gamma\) de \(s\) à \(t\) dans \(G_f\) :
- on sélectionne \(m\) le min de \(r_f((A,B))\) pour \((A,B) \in \gamma\);
- pour toute arrête \( (A,B) \in \gamma,\) :
- si \((A,B) \in E,\;\; f((A,B)) += m \);
- si \((A,B) \notin E,\;\; f((A,B)) -= m \);
Lorsque l'algorithme se termine, le flot \( f \) est alors le flot maximal.
Problème de la coupe minimale
Encore une fois, avant de pouvoir présenter le problème, il faut introduire de nouvelles définitions.
Coupe d'un graphe
Une coupe coupe \(C = (S,T) \) d'un graphe \(G = (V,E) \) est la donnée de deux sous-ensemble de sommets \(S\) et \(T\) tels que :
- les ensembles \(S\) et \(T\) couvrent \(V\) i.e. \(V = S \cup T \),
- les ensembles \(S\) et \(T\) soient disjoints i.e. \(S \cap T = \emptyset\).
Le cut-set \(Z_C\) d'une coupe \(C = (S,T) \) est l'ensemble des arrêtes coupées par la coupe i.e. \[Z_C := \{ (A,B) \in E, \textrm{ t. q. } A \in S \textrm{ et } B \in T \}. \]
Si \(G = (V,E,\omega) \) est un graphe pondéré, le poids \(\omega_C\) d'une coupe \(C\) est la somme des poids des arrêtes de \(Z_C\) i.e. \[\omega_C := \sum\limits_{(A,B) \in Z_C} \omega((A,B)). \]
Le problème de la coupe minimale consiste donc à trouver la (ou une des) coupe(s) de poids minimale(s) pour un graphe pondéré donné. Lorsque le graphe est un réseau de flot et qu'on impose les conditions \(s \in S\) et \(t \in T\), le théorème du max flow/min cut montre que le problème de flot maximal et le problème de coupe minimale sont directement reliés.
Max flow/min cut
Soit \( G = (V,E,c) \) un réseau de flot avec \(s,t \in V\). La valeur \(|f|\) du flot maximal de \(s\) à \(t\) est égal au poids \(\omega_C\) de la coupe minimal \(C = (S,T) \) telle que \(s \in S\) et \(t \in T \).
Tri topologique
Un tri topologique d'un graphe est défini uniquement sur un graphe acyclique orienté.
Tri topologique d'un graphe acyclique orienté
On dit que \(G = (V,E) \) est un graphe acyclique orienté si c'est un graphe orienté ne comportant aucun cycle.
On dit que \((v_n)_{1\leq n \leq \mathbf{Card}(V)}\) est un tri topologique de \(V\) si:
Un tri topologique n'est généralement pas unique. Par exemple, si on considère le graphe orienté acyclique suivant.
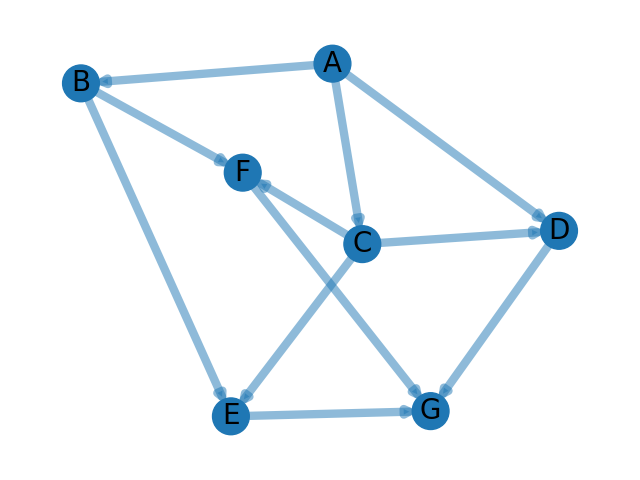
Alors, les numérotations : \[ [ A, B, C, D, E, F, G ],\] \[ [ A, C, D, B, F, E, G ],\] \[ [ A, C, B, E, F, D, G ],\] sont trois tris topologiques de \(G\).
Algorithmique
Pour trouver un tri topologique d'un graphe on utilise un algorithme de parcours DFS légèrement modifié. L'idée est d'associer à chaque sommet un temps \(t\). Au début, tous les sommets sont à temps \(0\). On initialise aussi un temps global à \(0\). À chaque fois qu'un sommet est complètement exploré, on augmente le temps global de \(1\) et le sommet complètement exploré (i.e. qui n'a plus aucun voisin non parcouru) se voit affecté le temps correspondant au temps global actuel. On lance alors des explorations du graphe en profondeur à partir des sommets dont le temps est encore à \(0\) jusqu'à ce que tous les sommets aient un temps strictement positif.
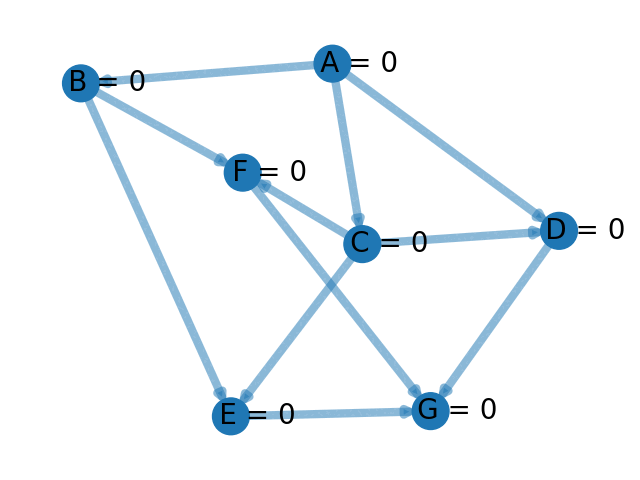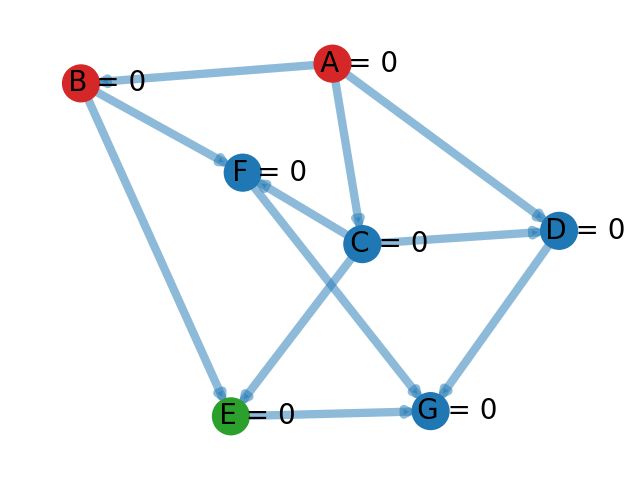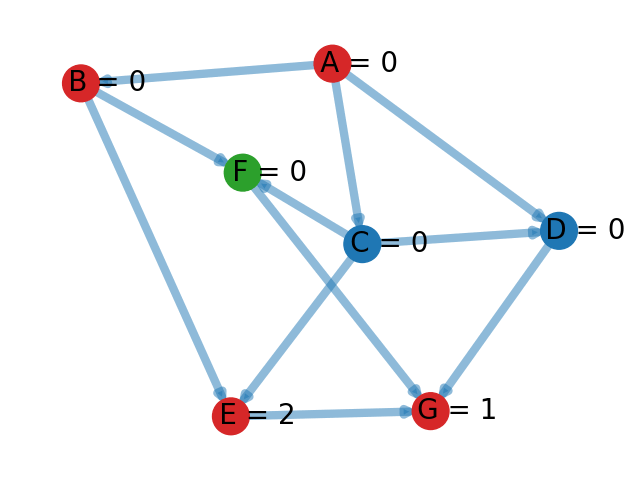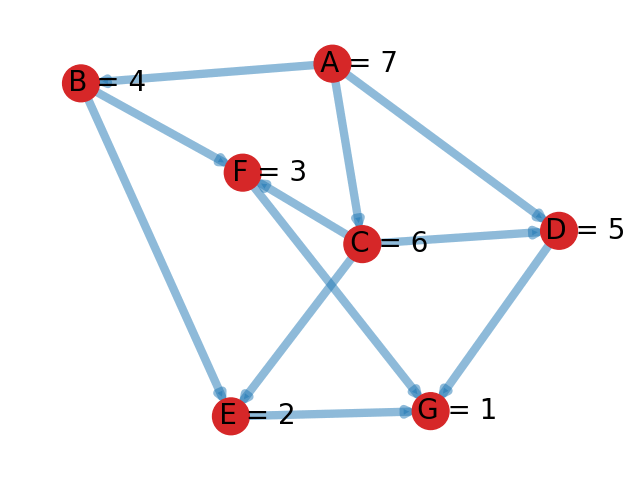
Il ne reste plus qu'à trier les sommets dans l'ordre décroissant de leur temps et on obtient un tri topologique. Pour l'exemple ci-dessus, on obtient le tri : \[ [ A, C, D, B, F, E, G ].\]
En python, on pourrait implémenter l'algorithme de recherche d'un tri topologique comme suit :
parcourus = []
times = dict()
#On initialise tous les temps des sommets à 0
for v in vertices:
times[v] = 0
#Et le temps global à 1
GlobalTime = 1
def explorerProfondeurModifie(sommetActuel):
parcourus.append(sommetActuel)
for voisin in Voisins(sommetActuel):
if(voisin not in parcourus):
explorerProfondeurModifie(voisin)
GlobalTime += 1
times[sommetActuel] = GlobalTime
existeSommetNul = True
while existeSommetNul:
SommetNul = -1
for sommet in vertices:
if(times[sommet] == 0):
SommetNul = sommet
break
if SommetNul == -1:
existeSommetNul = False
else:
explorerProfondeurModifie(SommetNul)
Problèmes
Problème 0: Chou, mouton et loup
Problème 1: Le solitaire

Le jeu du solitaire est un jeu qui, comme son nom l'indique, se joue seul. La configuration de départ est un plateau rempli de billes à l'exception du trou central (cf photo ci-dessus). Le but du jeu est d'arriver à la configuration finale inverse : une seule bille sur le plateau, au centre. Le seul coup légal dans ce jeu est de faire sauter une bille par dessus une autre bille. Dans ce cas, la bille qui a sauté est déplacée de deux cases. La bille qui s'est fait sauter par-dessus, elle, est retirée du plateau (voir la figure ci-dessous).
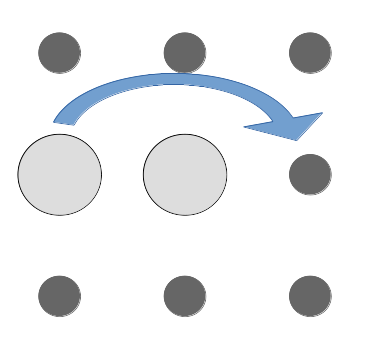
La bille de gauche saute par dessus la bille du centre.
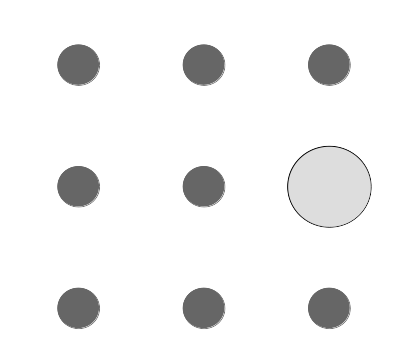
La bille de gauche se retrouve à droite, la bille du centre est retirée du plateau.
Ce coup ne peut être réalisé que verticalement ou horizontalement, il n'est pas possible de l'effectuer en diagonale. La case d'arrivée de la bille qui saute doit être libre pour réaliser ce coup.
Exercice :
- 1. Formaliser ce problème comme un graphe. Gagner le jeu doit se résumer à trouver un chemin sur un graphe.
- 2. Trouver une solution au solitaire en utilisant un algorithme de parcours de graphe.
- 3. Généraliser le problème : est-il possible d'atteindre n'importe quelle situation finale ? En partant de n'importe quelle situation finale ?
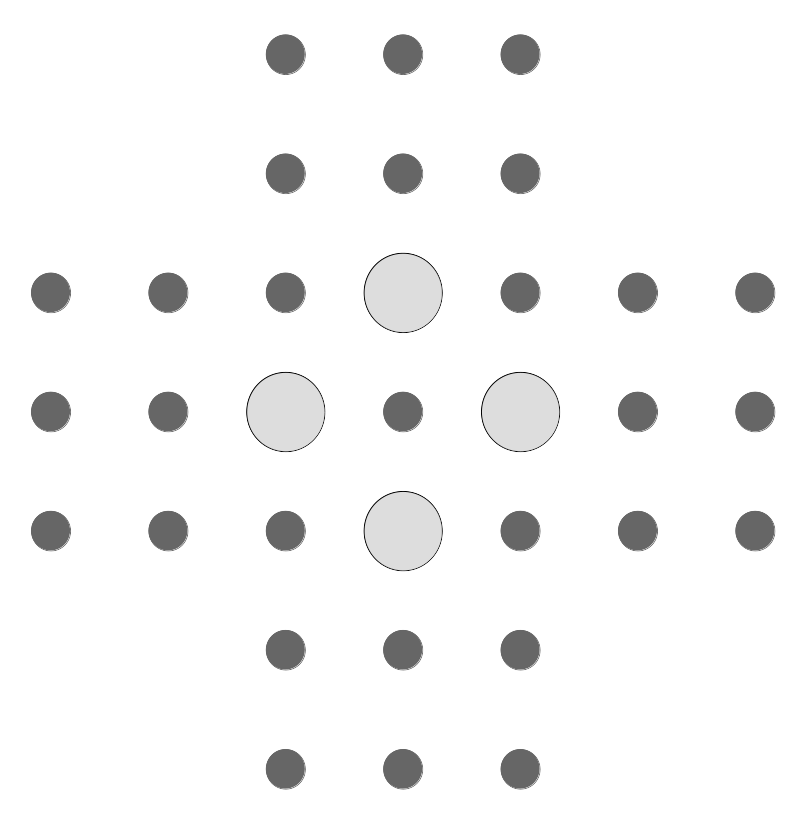
- 4. Trouver une situation initiale permettant d'arriver à la configuration suivante :
Au maximum, combien de billes possède une telle configuration initiale ?
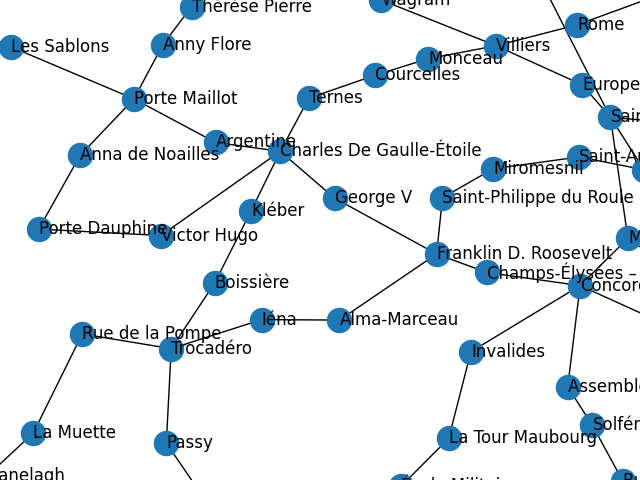
Problème 2: Itinéraire RATP
On souhaite coder un outil de recherche d'itinéraire en région parisienne en utilisant exclusivement les transports en commun et la marche. On utilise la base de données SQL téléchargeable ICI . La base de données est un extrait des données ouvertes et publiques trouvables sur data.gouv.fr.
Exercice :
- 1. Afficher le graphe du réseau RATP avec networkx. On utilisera sqlite3 pour récupérer les données dans la base de donnée.
- 2. Formaliser le problème sous la forme d'un graphe pondéré. Attention : on peut passer d'une station à l'autre en marchant.
- 3. En utilisant un algorithme type Bellman-Ford, trouver le chemin le plus court en transport en commun entre deux stations. On supposera que changer de ligne de transport prend 5 minutes et que, sur une même ligne, passer d'une station à l'autre prend 2 minutes.
- 4. Même question mais cette fois, on cherche le trajet le plus court entre deux points de l'espace (pas forcément des stations). On considère que la vitesse de marche est de 4km/h.
- 5. Créer une interface utilisateur pour permettre à un utilisateur ne connaissant pas python d'utiliser les fonctions précédentes.
Problème 3 : répartition minière

Une entreprise veut exploiter une carrière de fer. L'entreprise souhaite savoir combien de minerai de fer elle peut extraire en fonction de ce que les entreprises locales sont prêtes à lui acheter. En faisant un sondage, on obtient les informations suivantes (exprimées en tonnes par mois notés \(t/m\) ) :
- L'entreprise \(A\) peut transformer \(300 t/m\) de minerai de fer en acier brut.
- L'entreprise \(B\) peut transformer \(120 t/m\) de minerai de fer en acier raffiné.
- L'entreprise \(C\) peut transformer \(230 t/m\) de minerai de fer en acier brut.
- L'entreprise \(D\) peut transformer \(80t/m\) d'acier raffiné en pièces automobiles.
- L'entreprise \(E\) peut transformer \(260 t/m\) d'acier brut en quincaillerie.
- L'entreprise \(G\) peut transformer \(300 t/m\) de quincaillerie en pièces automobiles.
- L'entreprise \(H\) peut transformer \(170 t/m\) d'acier raffiné en quincaillerie.
- L'entreprise \(I\) peut transformer \(110 t/m\) d'acier raffiné et \(130t/m \) d'acier brut en plaques d'acier.
- L'entreprise \(J\) peut transformer \(260 t/m\) de plaques d'acier en pièces automobiles.
- L'entreprise \(K\) peut transformer \(180 t/m\) d'acier brut en acier raffiné.
- L'entreprise \(L\) rachète toute pièce automobile de la région, elle a le monopole complet.
L'entreprise souhaiterait savoir combien de tonnes de minerai de fer elle pourrait espérer vendre par mois étant donné l'écosystème régional.
Exercice :
- 1. Reformuler le problème comme un problème de flot maximal (Attention : il faut bien choisir ce que sont les sommets du graphe).
- 2. À l'aide d'un algorithme de Ford-Fulkerson (ou d'un autre algorithme de max flow externe comme scipy), répondre à la question de l'entreprise.
- 3. Si l'entreprise \(I\) ferme quel serait l'impact sur la demande de minerai ? Même question pour l'entreprise \(H\).
- 4. Trouver une coupe minimale du graphe obtenu. Que représente les deux sous-ensembles de sommets obtenus ?
Problème 4 : Patisseries

Un patissier cherche à optimiser son temps pour la confection des deux recettes suivantes :
Tarte aux fraises
- Couper les fraises (10 min)
- Préparer la crême patissière (30 min)
- Préparer la pâte à tarte (5 min)
- Cuire la pâte (45 min)
- Attendre que la pâte refroidisse (30 min)
- Dresser la tarte avec la crême et les fraises (10 min)
Choux à la crême
- Préparer la crême patissière (30 min)
- Préparer la pâte à choux (15 min)
- Laisser reposer la pâte (60 min)
- Cuire les choux (25 min)
- Remplir les choux avec la crême (20 min)
Exercice :
- 1. Dessiner un graphe modélisant le problème.
- 2. On suppose d'abord que le patissier dispose de suffisamment de commis (et de fours) pour réaliser toutes les étapes simultanément à condition que les prérequis de l'étape soient satisfaits. Utiliser un tri topologique pour proposer un planning. Est-ce que le planning obtenu est optimal ?
- 3. On suppose maintenant que le patissier ne dispose que d'un seul four, il ne peut donc pas y avoir deux cuissons en simultané. Proposer un planning correspondant à cette nouvelle contrainte.
- 4. Même question mais en supposant que le patissier n'a qu'un seul commis. Dans cette situation, seul deux étapes "actives" peuvent être effectuées en simultané.